Collaboration diagram for Numerical algorithms:

Modules
	Discrete Fourier transforms

	Classes and functions for B-spline interpolation.

Files
file	determinant.h
	Declaration of stir::determinant() function for matrices.

file	divide.h
	implementation of stir::divide

file	divide.inl
	implementation of stir::divide

file	erf.h

file	FastErf.h
	Implementation of an erf interpolation.

file	FastErf.inl
	Implementation of an erf interpolation.

file	ieeefp.h
	Definition of work-around macros STIR_isnan and STIR_finite for a few non-portable IEEE floating point functions.

file	integrate_discrete_function.h
	Declaration of stir::integrate_discrete_function function.

file	IR_filters.h
	Implementation of the IIR and FIR filters.

file	IR_filters.inl
	implements the IR_filters

file	MatrixFunction.h
	Declaration of functions for matrices.

file	MatrixFunction.inl
	Implementation of functions for matrices.

file	max_eigenvector.h
	Declaration of functions for computing eigenvectors.

file	norm.h
	Declaration of the stir::norm(), stir::norm_squared() functions and stir::NormSquared unary function.

file	norm.inl
	Implementation of the stir::norm(), stir::norm_squared() functions and stir::NormSquared unary function.

file	overlap_interpolate.h
	Declaration of stir::overlap_interpolate.

file	overlap_interpolate.inl
	Implementation of inline versions of stir::overlap_interpolate.

file	sampling_functions.h
	Sampling functions (currently only stir::sample_function_on_regular_grid)

file	stir_NumericalRecipes.h
	functions to convert from data in Numerical Recipes format to STIR arrays.

file	linear_extrapolation.h
	stir::linear_extrapolation

file	more_interpolators.h
	Functions to interpolate data.

file	more_interpolators.inl
	Functions to interpolate data.

file	determinant.cxx
	Implementation of stir::determinant() function for matrices.

Namespaces
	stir
	Namespace for the STIR library (and some/most of its applications)

Classes
class	stir::PullLinearInterpolator< elemT >
	A function object to pull interpolated values from the input array into the grid points of the output array. More...

class	stir::PushTransposeLinearInterpolator< elemT >
	A function object to push values at the grid of the input array into the output array. More...

class	stir::PullNearestNeighbourInterpolator< elemT >
	A function object to pull interpolated values from the input array into the grid points of the output array. More...

class	stir::PushNearestNeighbourInterpolator< elemT >
	A function object to push values at the grid of the input array into the output array. More...

Functions
template<class elemT >
elemT	stir::determinant (const Array< 2, elemT > &m)
	Compute the determinant of a matrix. More...

template<class NumeratorIterT , class DenominatorIterT , class small_numT >
void	stir::divide (const NumeratorIterT &numerator_begin, const NumeratorIterT &numerator_end, const DenominatorIterT &denominator_begin, const small_numT small_num)
	division of two ranges, 0/0 = 0 More...

template<typename elemT >
elemT	stir::integrate_discrete_function (const std::vector< elemT > &coordinates, const std::vector< elemT > &values, const int interpolation_order=1)
	numerical integration of a 1D functionThis is a simple integral implementation using rectangular (=0) or trapezoidal (=1) approximation. It currently integrates over the complete range specified. More...

template<class elemT >
Succeeded	stir::absolute_max_eigenvector_using_power_method (elemT &max_eigenvalue, Array< 1, elemT > &max_eigenvector, const Array< 2, elemT > &m, const Array< 1, elemT > &start, const double tolerance=.01, const unsigned long max_num_iterations=10000UL)
	Compute the eigenvalue with the largest absolute value and corresponding eigenvector of a matrix by using the power method. More...

template<class elemT >
Succeeded	stir::absolute_max_eigenvector_using_shifted_power_method (elemT &max_eigenvalue, Array< 1, elemT > &max_eigenvector, const Array< 2, elemT > &m, const Array< 1, elemT > &start, const elemT shift, const double tolerance=.03, const unsigned long max_num_iterations=10000UL)
	Compute the eigenvalue with the largest absolute value and corresponding eigenvector of a matrix by using the shifted power method. More...

template<class elemT >
Succeeded	stir::max_eigenvector_using_power_method (elemT &max_eigenvalue, Array< 1, elemT > &max_eigenvector, const Array< 2, elemT > &m, const Array< 1, elemT > &start, const double tolerance=.03, const unsigned long max_num_iterations=10000UL)
	Compute the eigenvalue with the largest value and corresponding eigenvector of a matrix by using the power method. More...

template<typename T >
void	stir::overlap_interpolate (VectorWithOffset< T > &out_data, const VectorWithOffset< T > &in_data, const float zoom, const float offset, const bool assign_rest_with_zeroes=true)
	'overlap' interpolation (i.e. count preserving) for vectors. More...

template<typename out_iter_t , typename out_coord_iter_t , typename in_iter_t , typename in_coord_iter_t >
void	stir::overlap_interpolate (const out_iter_t out_begin, const out_iter_t out_end, const out_coord_iter_t out_coord_begin, const out_coord_iter_t out_coord_end, const in_iter_t in_begin, in_iter_t in_end, const in_coord_iter_t in_coord_begin, const in_coord_iter_t in_coord_end, const bool only_add_to_output=false, const bool assign_rest_with_zeroes=true)
	'overlap' interpolation for iterators, with arbitrary 'bin' sizes. More...

template<class FunctionType , class elemT , class positionT >
void	stir::sample_function_on_regular_grid (Array< 3, elemT > &out, FunctionType func, const BasicCoordinate< 3, positionT > &offset, const BasicCoordinate< 3, positionT > &step)
	Generic function to get the values of a 3D function on a regular grid. More...

template<typename elemT , typename FunctionType , typename Lambda >
void	stir::sample_function_using_index_converter (Array< 3, elemT > &out, FunctionType func, Lambda &&index_converter)
	Generic function to get the values of a 3D function on a grid. More...

template<class elemT , class positionT >
elemT	stir::pull_nearest_neighbour_interpolate (const Array< 3, elemT > &in, const BasicCoordinate< 3, positionT > &point_in_input_coords)
	Pull value from the input array using nearest neigbour interpolation. More...

template<int num_dimensions, class elemT , class positionT , class valueT >
void	stir::push_nearest_neighbour_interpolate (Array< num_dimensions, elemT > &out, const BasicCoordinate< num_dimensions, positionT > &point_in_output_coords, valueT value)
	Push value into the output array using nearest neigbour interpolation. More...

template<class elemT , class positionT >
elemT	stir::pull_linear_interpolate (const Array< 3, elemT > &in, const BasicCoordinate< 3, positionT > &point_in_input_coords)
	Returns an interpolated value according to point_in_input_coords.

template<class elemT , class positionT , class valueT >
void	stir::push_transpose_linear_interpolate (Array< 3, elemT > &out, const BasicCoordinate< 3, positionT > &point_in_output_coords, valueT value)
	Push value into the output array using the transpose of linear interpolation.

Array< 3, float >	stir::extend_segment (const SegmentBySinogram< float > &segment, const int view_extension=5, const int axial_extension=5, const int tangential_extension=5)
	Extension of direct projection data. More...

functions specific for 1D Arrays
template<class elemT >
elemT	stir::inner_product (const Array< 1, elemT > &v1, const Array< 1, elemT > &v2)
	Inner product of 2 1D arrays. More...

template<class elemT >
double	stir::angle (const Array< 1, elemT > &v1, const Array< 1, elemT > &v2)
	angle between 2 1D arrays

Detailed Description

Function Documentation

◆ extend_segment()

Array< 3, float > stir::extend_segment	(	const SegmentBySinogram< float > &	segment,
		const int	view_extension = `5`,
		const int	axial_extension = `5`,
		const int	tangential_extension = `5`
	)

Extension of direct projection data.

Functions that extend the given sinogram or segment in the view direction taking periodicity into account, if exists. If the sinogram is not symmetric in tangential position, the values are extrapolated by nearest neighbour known values.

This is probably only useful before calling interpolation routines, or for FORE.

Generic function to extend a segment in any or all directions. Axially and tangentially, the segment is filled with the nearest existing value. In view direction, the function wraps around for stir::ProjData that cover 180° or 360° degrees, and throws an error for other angular coverages.

Parameters

[in,out]	segment	segment to be extended.
[in]	view_extension	how many views to add either side of the segment
[in]	axial_extension	how many axial bins to add either side of the segment
[in]	tangential_extension	how many tangential bins to add either side of the segment

References _PI, stir::VectorWithOffset< Array< num_dimensions - 1, elemT > >::get_max_index(), stir::VectorWithOffset< Array< num_dimensions - 1, elemT > >::get_min_index(), stir::Segment< elemT >::get_proj_data_info_sptr(), and stir::Array< num_dimensions, elemT >::grow().

◆ determinant()

template<class elemT >

elemT stir::determinant ( const Array< 2, elemT > & m )

Compute the determinant of a matrix.

Matrix indices can start from any number.

Todo:: Only works for low dimensions for now.

Referenced by stir::Shape3DWithOrientation::get_volume_of_unit_cell().

◆ divide()

template<class NumeratorIterT , class DenominatorIterT , class small_numT >

void stir::divide	(	const NumeratorIterT &	numerator_begin,
		const NumeratorIterT &	numerator_end,
		const DenominatorIterT &	denominator_begin,
		const small_numT	small_num
	)

inline

division of two ranges, 0/0 = 0

This function sets 0/0 to 0 (not the usual NaN). It is for instance useful in Poisson log-likelihood computation.

Because of potential numerical rounding problems, we test if a number is 0 by comparing its absolute value with a small value, which is determined by multiplying the maximum in the numerator range with small_num.

Warning: This function does not test for non-zero numbers by 0. Results in that case will likely depend on your processor and/or compiler settings.

Referenced by stir::BinNormalisationPETFromComponents::apply(), stir::KOSMAPOSLReconstruction< TargetT >::compute_kernelised_image(), and stir::OSMAPOSLReconstruction< TargetT >::update_estimate().

◆ integrate_discrete_function()

template<typename elemT >

elemT stir::integrate_discrete_function	(	const std::vector< elemT > &	coordinates,
		const std::vector< elemT > &	values,
		const int	interpolation_order = `1`
	)

inline

numerical integration of a 1D functionThis is a simple integral implementation using rectangular (=0) or trapezoidal (=1) approximation. It currently integrates over the complete range specified.

Parameters

coordinates	Coordinates at which the function samples are given
values	Function values
interpolation_order	has to be 0 or 1

Warning: Type elemT should not be an integral type.

Referenced by stir::PlasmaData::get_sample_data_in_frames(), and stir::integrate_discrete_functionTests::run_tests().

◆ inner_product()

template<class elemT >

elemT stir::inner_product	(	const Array< 1, elemT > &	v1,
		const Array< 1, elemT > &	v2
	)

inline

Inner product of 2 1D arrays.

This returns the sum of multiplication of elements of conjugate(v1) and v2.

Implementation is appropriate for complex numbers.

Arguments must have the same index range.

◆ absolute_max_eigenvector_using_power_method()

template<class elemT >

Succeeded stir::absolute_max_eigenvector_using_power_method	(	elemT &	max_eigenvalue,
		Array< 1, elemT > &	max_eigenvector,
		const Array< 2, elemT > &	m,
		const Array< 1, elemT > &	start,
		const double	tolerance = `.01`,
		const unsigned long	max_num_iterations = `10000UL`
	)

inline

Compute the eigenvalue with the largest absolute value and corresponding eigenvector of a matrix by using the power method.

Parameters

[out]	max_eigenvalue	will be set to the eigenvalue found
[out]	max_eigenvector	will be set to the eigenvector found, and is normalised to 1 (using the l2-norm). The sign choice is determined by normalising the largest element in the eigenvector to 1.
[in]	m	is the input matrix
[in]	start	is a starting vector for the iterations
[in]	tolerance	determines when iterations can stop
[in]	max_num_iterations	is used to prevent an infinite loop

Returns: Succeeded::yes if max_num_iterations was not reached. However, you probably want to check if the norm of the difference between m.max_eigenvector and max_eigenvalue*max_eigenvector is small (compared to max_eigenvalue).

Computation uses the power method, see for instance http://www.maths.lth.se/na/courses/FMN050/FMN050-05/eigenE.pdf.

The method consists in computing

$v^{n+1}=m.v^{n}$

$v^{n+1}/=\mathrm{norm}(v^{n+1})$

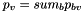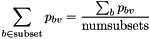with $v^{0}=\mathrm{start}$ for $ n$ big enough such that 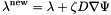$\mathrm{norm}(v^{n+1}-v^{n})$ becomes smaller than tolerance. The eigenvalue is then computed using the Rayleigh quotient

$v.m.v \over v.v$

This will converge to the eigenvector which has the largest absolute eigenvalue. The method fails when the matrix has more than 1 largest absolute eigenvalue (e.g. with opposite sign).

References stir::abs_max_element(), stir::VectorWithOffset< T >::begin(), stir::VectorWithOffset< T >::end(), stir::inner_product(), stir::Array< num_dimensions, elemT >::is_regular(), stir::matrix_multiply(), stir::norm(), stir::norm_squared(), stir::VectorWithOffset< T >::size(), and stir::square().

Referenced by stir::absolute_max_eigenvector_using_shifted_power_method(), and stir::max_eigenvector_using_power_method().

◆ absolute_max_eigenvector_using_shifted_power_method()

template<class elemT >

Succeeded stir::absolute_max_eigenvector_using_shifted_power_method	(	elemT &	max_eigenvalue,
		Array< 1, elemT > &	max_eigenvector,
		const Array< 2, elemT > &	m,
		const Array< 1, elemT > &	start,
		const elemT	shift,
		const double	tolerance = `.03`,
		const unsigned long	max_num_iterations = `10000UL`
	)

inline

Compute the eigenvalue with the largest absolute value and corresponding eigenvector of a matrix by using the shifted power method.

See also: absolute_max_eigenvector_using_shifted_power_method().

The current method calls the normal power method for m-shift*I and shifts the eigenvalue back to the eigenvalue for m.

This method can be used to enhance the convergence rate if you know more about the eigenvalues. It can also be used to find another eigenvalue by shifting with the maximum eigenvalue.

References stir::absolute_max_eigenvector_using_power_method(), stir::diagonal_matrix(), stir::error(), stir::VectorWithOffset< T >::get_min_index(), and stir::VectorWithOffset< T >::size().

Referenced by stir::max_eigenvector_using_power_method().

◆ max_eigenvector_using_power_method()

template<class elemT >

Succeeded stir::max_eigenvector_using_power_method	(	elemT &	max_eigenvalue,
		Array< 1, elemT > &	max_eigenvector,
		const Array< 2, elemT > &	m,
		const Array< 1, elemT > &	start,
		const double	tolerance = `.03`,
		const unsigned long	max_num_iterations = `10000UL`
	)

inline

Compute the eigenvalue with the largest value and corresponding eigenvector of a matrix by using the power method.

Warning: This assumes that all eigenvalues are real.

See also: absolute_max_eigenvector_using_shifted_power_method().

Parameters

[in] m is the input matrix, which has to be real-symmetric

This will attempt to find the eigenvector which has the largest eigenvalue. The method fails when the matrix has a negative eigenvalue of the same magnitude as the largest eigenvalue.

Todo:: the algorithm would work with hermitian matrices, but the code needs one small adjustment.

References stir::absolute_max_eigenvector_using_power_method(), and stir::absolute_max_eigenvector_using_shifted_power_method().

Referenced by stir::RigidObject3DTransformation::find_closest_transformation().

◆ overlap_interpolate() [1/2]

template<typename T >

void stir::overlap_interpolate	(	VectorWithOffset< T > &	out_data,
		const VectorWithOffset< T > &	in_data,
		const float	zoom,
		const float	offset,
		const bool	assign_rest_with_zeroes
	)

'overlap' interpolation (i.e. count preserving) for vectors.

This is an implementation of 'overlap' interpolation on arbitrary data types (using templates).

This type of interpolation considers the data as the samples of a step-wise function. The interpolated array again represents a step-wise function, such that the counts (i.e. integrals) are preserved.

Parameters

zoom	The spacing between the new points is determined by the 'zoom' parameter: e.g. zoom less than 1 stretches the bin size with a factor 1/zoom.
offset	(measured in 'units' of the in_data) allows to shift the range of values you want to compute. In particular, having positive offset shifts the data to the left (if in_data and out_data have the same range of indices). Note that a similar (but less general) effect to using 'offset' can be achieved by adjusting the min and max indices of the out_data.
assign_rest_with_zeroes	If `false` does not set values in `out_data` which do not overlap with `in_data`. If `true` those data are set to 0. (The effect being the same as first doing `out_data.fill(0)` before calling overlap_interpolate).

For an index x_out (in out_data coordinates), the corresponding in_data coordinates is x_in = x_out/zoom + offset (The convention is used that the 'bins' are centered around the coordinate value.)

Warning: when T involves integral types, there is no rounding but truncation.

Examples:

in_data = {a,b,c,d} indices from 0 to 3
zoom = .5
offset = .5
out_data = {a+b, c+d} indices from 0 to 1

in_data = {a,b,c,d} indices from 0 to 3
zoom = .5
offset = -.5
out_data = {a,b+c,d} indices from 0 to 2

in_data = {a,b,c} indices from -1 to 1
zoom = .5
offset = 0
out_data = {a/2, a/2+b+c/2, c/2} indices from -1 to 1

Implementation details:

Because this implementation works for arbitrary (numeric) types T, it is slightly more complicated than would be necessary for (say) floats. In particular,

we do our best to avoid creating temporary objects of type T
we zero values by using multiplication with 0
(actually we use T::operator*=(0)). This is to allow the case where T::operator=(int) does not exist (in particular, in our higher dimensional arrays).

History:

first version by Kris Thielemans with suggestions by Alexey Zverovich. (loosely based on a 1D version by Claire Labbe)

See also: overlap_interpolate(const out_iter_t out_begin, const out_iter_t out_end, const out_coord_iter_t out_coord_begin, const out_coord_iter_t out_coord_end, const in_iter_t in_begin, in_iter_t in_end, const in_coord_iter_t in_coord_begin, const in_coord_iter_t in_coord_end, const bool only_add_to_output=false, const bool assign_rest_with_zeroes)

Referenced by stir::ArcCorrection::set_up(), and stir::zoom_image().

◆ overlap_interpolate() [2/2]

template<typename out_iter_t , typename out_coord_iter_t , typename in_iter_t , typename in_coord_iter_t >

void stir::overlap_interpolate	(	const out_iter_t	out_begin,
		const out_iter_t	out_end,
		const out_coord_iter_t	out_coord_begin,
		const out_coord_iter_t	out_coord_end,
		const in_iter_t	in_begin,
		in_iter_t	in_end,
		const in_coord_iter_t	in_coord_begin,
		const in_coord_iter_t	in_coord_end,
		const bool	only_add_to_output = `false`,
		const bool	assign_rest_with_zeroes = `true`
	)

inline

'overlap' interpolation for iterators, with arbitrary 'bin' sizes.

This type of interpolation considers the data as the samples of a step-wise function. The interpolated array again represents a step-wise function, such that the counts (i.e. integrals) are preserved.

In and out data are specified using iterators. For each, there is also a pair of iterators specifying the coordinates of the edges of the 'bins' (or 'boxes') in some arbitrary coordinate system (common between in and out parameters of course). Note that there should be one more coordinate than data (i.e. you have to specify the last edge as well). This is (only) checked with assert() statements.

Parameters

only_add_to_output	If `false` will overwrite any data present in the output (aside from possibly the tails: see `assign_rest_with_zeroes`). If `true`, results will be added to the data.
assign_rest_with_zeroes	If `false` does not set values in the `out` range which do not overlap with `in` range. If `true` those data are set to 0.

Warning: when the out iterators point to an integral type, there is no rounding but truncation.

Examples:: Given 2 arrays and zoom and offset parameters
Array<1,float> in = ...;
Array<1,float> out = ...;
float zoom = ...; float offset = ...;
the following pieces of code should give the same result (this is tested in test_interpolate):
overlap_interpolate(out, in, zoom, offset, true);
and
Array<1,float> in_coords(in.get_min_index(), in.get_max_index()+1);
for (int i=in_coords.get_min_index(); i<=in_coords.get_max_index(); ++i)
in_coords[i]=i-.5F;
Array<1,float> out_coords(out.get_min_index(), out.get_max_index()+1);
for (int i=out_coords.get_min_index(); i<=out_coords.get_max_index(); ++i)
out_coords[i]=(i-.5F)/zoom+offset;
overlap_interpolate(out.begin(), out.end(),
out_coords.begin(), out_coords.end(),
in.begin(), in.end(),
in_coords.begin(), in_coords.end()
);

Implementation details:

Because this implementation works for arbitrary (numeric) types, it is slightly more complicated than would be necessary for (say) floats. In particular,

we do our best to avoid creating temporary objects
we zero values by using multiplication with 0. This is to allow the case where assignment with an int (or float) does not exist (in particular, in our higher dimensional arrays).

The implementation is inline to avoid problems with template instantiations.

History:

first version by Kris Thielemans

◆ sample_function_on_regular_grid()

template<class FunctionType , class elemT , class positionT >

void stir::sample_function_on_regular_grid	(	Array< 3, elemT > &	out,
		FunctionType	func,
		const BasicCoordinate< 3, positionT > &	offset,
		const BasicCoordinate< 3, positionT > &	step
	)

inline

Generic function to get the values of a 3D function on a regular grid.

Parameters

[in,out]	out	array that will be filled with the function values. Its dimensions are used to find the coordinates where to sample the function (see below).
[in]	func	function to sample
[in]	offset	offset to use for coordinates (see below)
[in]	step	step size to use for coordinates (see below)

Symbolically, this function does the following computation for every index in the array

out(index) = func(index * step - offset)

requirement for type FunctionType: Due to the calling sequence above, the following has to be defined
elemT FunctionType::operator(const BasicCoordinate<3, positionT>&)

Todo:: At the moment, only the 3D version is implemented, but this could be templated.

References stir::IndexRange< num_dimensions >::get_regular_range(), and stir::warning().

◆ sample_function_using_index_converter()

template<typename elemT , typename FunctionType , typename Lambda >

void stir::sample_function_using_index_converter	(	Array< 3, elemT > &	out,
		FunctionType	func,
		Lambda &&	index_converter
	)

inline

Generic function to get the values of a 3D function on a grid.

Parameters

[in,out]	out	array that will be filled with the function values. Its dimensions are used to find the coordinates where to sample the function (see below).
[in]	func	function to sample
[in]	index_converter	a lambda function converting indices in the out array to coordinates where the function shall be sampled

requirement for type FunctionType: Due to the calling sequence above, the following has to be defined
elemT FunctionType::operator(const BasicCoordinate<3, positionT>&)

Todo:: At the moment, only the 3D version is implemented, but this could be templated.

References stir::IndexRange< num_dimensions >::get_regular_range(), and stir::warning().

◆ pull_nearest_neighbour_interpolate()

template<class elemT , class positionT >

elemT stir::pull_nearest_neighbour_interpolate	(	const Array< 3, elemT > &	in,
		const BasicCoordinate< 3, positionT > &	point_in_input_coords
	)

Pull value from the input array using nearest neigbour interpolation.

Adds value to the grid point nearest to point_in_output_coords

References stir::VectorWithOffset< T >::get_max_index(), stir::VectorWithOffset< T >::get_min_index(), and stir::round().

◆ push_nearest_neighbour_interpolate()

template<int num_dimensions, class elemT , class positionT , class valueT >

void stir::push_nearest_neighbour_interpolate	(	Array< num_dimensions, elemT > &	out,
		const BasicCoordinate< num_dimensions, positionT > &	point_in_output_coords,
		valueT	value
	)

Push value into the output array using nearest neigbour interpolation.

Adds value to the grid point nearest to point_in_output_coords

References stir::VectorWithOffset< Array< num_dimensions - 1, elemT > >::get_max_index(), stir::VectorWithOffset< Array< num_dimensions - 1, elemT > >::get_min_index(), and stir::round().

Modules

Files

Namespaces

Classes

Functions

functions specific for 1D Arrays

Detailed Description

Function Documentation

◆ extend_segment()

◆ determinant()

◆ divide()

◆ integrate_discrete_function()

◆ inner_product()

◆ absolute_max_eigenvector_using_power_method()

◆ absolute_max_eigenvector_using_shifted_power_method()

◆ max_eigenvector_using_power_method()

◆ overlap_interpolate() [1/2]

◆ overlap_interpolate() [2/2]

◆ sample_function_on_regular_grid()

◆ sample_function_using_index_converter()

◆ pull_nearest_neighbour_interpolate()

◆ push_nearest_neighbour_interpolate()